Las matemáticas están en todos lados. El autor de ciencia Ian Stewart publicó en 2013 las 17 ecuaciones que cambiaron al mundo. El resumen de estas ecuaciones y su importancia fue resumida por Paul Coxon, matemático, y por Larry Phillips, blogger de ciencia.

Estas son las ecuaciones que han moldeado a la humanidad en la historia:
1. El Teorema de Pitágoras
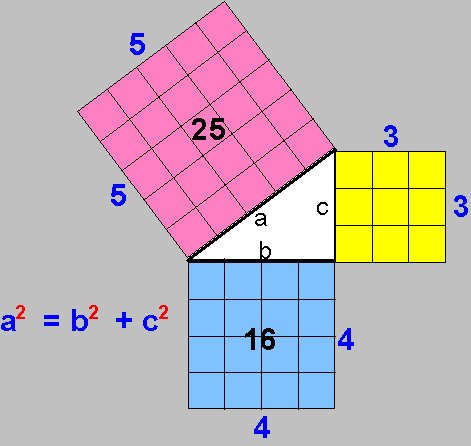
Este teorema es la fundación de nuestro entendimiento de la geometría. Describe la relación entre los lados de un triángulo rectángulo: el cuadrado de los lados más cortos es igual al cuadrado del lado más largo.
Esta relación distingue la geometría euclidiana de la geometría no-euclidiana de curvas. Por ejemplo, no se aplica el teorema a un triángulo rectángulo, dibujado en una esfera.
2. Logaritmos

Los logaritmos son lo opuesto o lo inverso de funciones exponenciales. Un logaritmo para una base particular te dice a qué potencia debes elevar la base para obtener el número. Por ejemplo, el logaritmo de 1000 en base 10 es 3, porque 1000 es igual a 10 a la potencia 3: 1000 = 10 al cubo = 10×10×10.
Así como lo contrario de la suma es la resta y la de la multiplicación la división, el cálculo de logaritmos es la operación inversa a la exponenciación de la base del logaritmo. Hasta el desarrollo de las computadoras, esta fue la manera más común de hacer grandes multiplicaciones de grandes números, acelerando los cálculos en física, astronomía e ingeniería.
3. Cálculo

La fórmula presentada aquí es la definición de un cálculo derivado. La derivada mide la velocidad a la que cambia la cantidad. Por ejemplo, podemos pensar en la velocidad como la derivada de una posición (si vas caminando a 3 millas por hora, entonces, cada hora has cambiado de posición por 3 millas).
Naturalmente, mucha de la ciencia se interesa en cómo cambian las cosas, y la derivada y la integral, los otros pilares del cálculo, tienen como fundamento cómo las matemáticas y los científicos entienden el cambio.
4. La Gravedad

Las leyes de la gravitación de Newton describen la fuerza de la gravedad entre dos objetos, F, en términos de una constante universal, G, las masas de los dos objetos, m1 y m2, y la distancia entre los objetos, r. La ley de Newton es una pieza muy importante de la historia de la ciencia, explica, casi perfectamente, por qué los planetas se mueven de la manera que lo hacen. También es muy importante su naturaleza universal, pues no sólo funciona en la Tierra sino en todo el universo. La Gravedad de Newton se sostuvo muy bien por 200 años, hasta la llegada de la teoría de Einstein.
5. La raíz cuadrada de -1

Los matemáticos siempre han expandido la idea que tenemos de lo que puede ser un número. Desde los números naturales, a los números negativos, las fracciones, los números reales, etc. La raíz cuadrada de -1, se escribe como i. Esta da origen a los números complejos.
Matemáticamente, los números complejos son supremamente elegantes. El álgebra trabaja perfectamente como lo queremos, cualquier ecuación tiene una solución de números complejos, una situación que no es verdad para los números reales: x2+4=0 no tiene una solución de números reales, pero tiene una solución compleja: la raíz cuadrada de -4, o 2i.
El cálculo se puede extender a los números complejos, y haciendo esto, encontramos simetrías increíbles y propiedades para esos números. Esas propiedades hacen a los números complejos esenciales en electrónica, por ejemplo.
6. Fórmula de Euler para poliedros
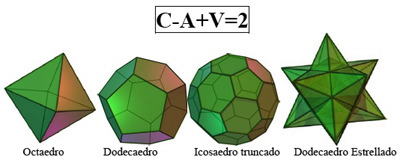
Los poliedros son las versiones tridimensionales de los polígonos, como el cubo. Las esquinas de un poliedro se llaman vértices, las líneas que conectan los vértices son sus aristas, y los polígonos que las cubren son las caras.
Un cubo tiene 8 vértices, 12 orillas y seis caras. Si junto los vértices y las caras, y resto las aristas, tengo 8+6-12=2. La fórmula de Euler establece que en tanto que tu poliedro se comporte bien, de alguna manera, si agregas los vértices y las caras, y restas las aristas, siempre tendrás 2. Esto será cierto si tu poliedro tiene 4, 8, 12, 20 o cualquier número de caras.
Su descubrimiento fue uno de los primeros ejemplos de lo que ahora se llama “invariante topológico”, algún número o propiedad compartida por una clase de formas que son similares entre ellas. Toda la clase de poliedros “bien portados” tienen V+C-A=2.
Esta observación, junto con la solución de Euler al problema de los puentes de Koningsburg, pavimentó el camino a la topología, una rama de la matemática esencial para la física moderna.
7. Distribución de probabilidad
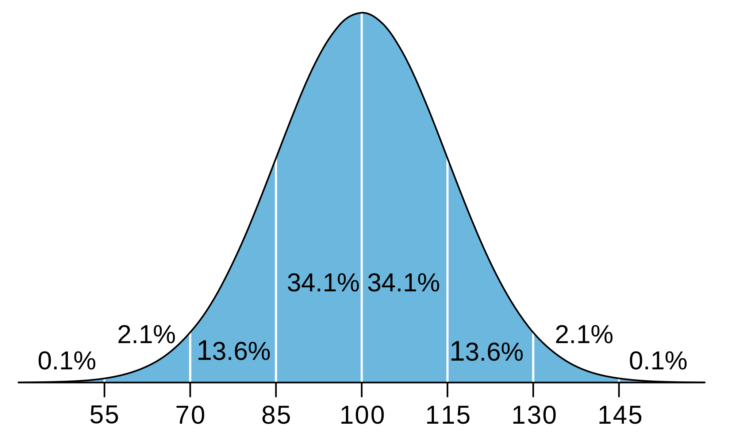
En teoría de la probabilidad y estadística, la distribución de probabilidad de una variable aleatoria es una función que asigna a cada suceso definido sobre la variable aleatoria la probabilidad de que dicho suceso ocurra.
Es usada en física, biología y en ciencias sociales para modelar distintas propiedades. Una de las razones por las que la curva aparece tan seguido es que describe el comportamiento de grupos grandes de procesos independientes.
8. Ecuación de onda
Esta es una ecuación diferencial, o una ecuación que describe cómo una propiedad cambiante en el tiempo en términos de la derivada de esa propiedad. La ecuación de onda describe el comportamiento de las ondas, una cuerda de guitarra que vibra, las ondas en el agua, la luz que sale de un foco, etc.
Era una ecuación diferencial temprana y las técnicas desarrolladas para resolverla abrieron la puerta a entender las ecuaciones diferenciales también.
9. Transformada de Fourier

Esta ecuación es esencial para entender estructuras de onda más complejas, como el lenguaje. Dada una función complicada de onda, una grabación de una persona hablando, la transformada de Fourier nos permite descomponer la función desordenada en una combinación de varias ondas simples, simplificando mucho el análisis.
Esta ecuación está en el corazón del procesamiento de señales y análisis, así como compresión de datos.
10. Ecuaciones de Navier-Stokes

Como las ecuaciones de onda, esta es una ecuación diferencial. Las ecuaciones de Navier-Stokes describen el comportamiento de los fluidos, agua moviéndose en un tubo, aire fluyendo sobre el ala de un avión, o humo saliendo de un cigarro.
Aunque hay computadoras que permiten simular movimiento de fluidos, todavía es una cuestión abierta si es posible construir una solución matemática exacta a las ecuaciones.
11. Ecuaciones de Maxwell

Las ecuaciones de Maxwell son al electromagnetismo lo que las leyes de Newton a la mecánica clásica. Son la base de nuestra explicación de cómo el electromagnetismo trabaja a gran escala. La física moderna descansa en la explicación cuántica del electromagnetismo. Las ecuaciones de Maxwell, originalmente 20 ecuaciones, describen por completo los fenómenos electromagnéticos. y recogen los descubrimientos de Coulomb, Gauss, Ampere, Faraday y otros.
12. Segunda ley de la termodinámica
Esta ley dice que “La cantidad de entropía del universo tiende a incrementarse en el tiempo”. La entropía en termodinámica es la medida de lo desordenado de un sistema. Un sistema que empieza ordenado, de manera dispareja, digamos una región caliente junto a una región fría, siempre tenderá a romper los límites, con calor fluyendo de lo caliente a la frío hasta que quedan distribuidos equitativamente.
Esta ley es uno de los pocos casos en física donde el tiempo importa: la mayoría de los procesos físicos son reversibles, podemos correr las ecuaciones al revés sin tener problemas. La segunda ley, sólo va en una dirección. Si ponemos un cubo de hielo en un café caliente, siempre veremos el hielo derretirse y nunca veremos el café congelarse.
13. La relatividad

Einstein alteró el curso de la física radicalmente con sus teorías especial y general de la relatividad. La clásica ecuación E=mc2 establece que la materia y la energía son equivalentes entre sí. La relatividad especial trajo ideas como que la velocidad de la luz es un límite de la velocidad universal y que el tiempo pasa de manera distinta para la gente que se mueve a diferentes velocidades.
La relatividad general describe la gravedad como un pliegue del espacio y el tiempo en sí mismos, y fue el primer gran cambio a nuestro entendimiento de la gravedad desde la ley de Newton. La relatividad general es esencial para nuestro entendimiento de los orígenes, la estructura y el destino del universo.
14. Ecuación de Schrodinger

Esta es la ecuación principal en la mecánica cuántica. Así como la relatividad general explica nuestro universo a escala mayor, esta ecuación rige el comportamiento de los átomos y las partículas subatómicas.
La mecánica cuántica moderna y la relatividad general son las dos teorías científicas más exitosas en la historia, todas las observaciones científicas que se han hecho hasta ahora son consistentes con sus predicciones. La mecánica cuántica también es necesaria para la tecnología más moderna: energía nuclear, semiconductores de computadoras, y lásers se construyen alrededor del fenómeno cuántico.
15. Teoría de la Información
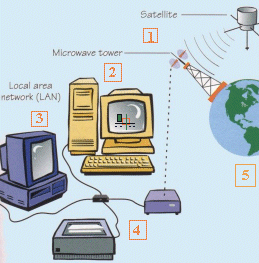
La ecuación dada aquí es la de entropía de Shannon. Así como la entropía termodinámica dada arriba, esta es una medida de desorden. En este caso, mide la información contenida en un mensaje, un libro, una foto JPEG enviada por Internet, o cualquier cosa que se pueda representar simbólicamente.
La entropía de Shannon en un mensaje muestra cuánto puede comprimirse el mensaje sin perder cierto contenido. La medida de entropía de Shannon inició el estudio matemático de la información, y sus resultados son básicos para entender cómo nos comunicamos en las redes.
16. Teoría del caos
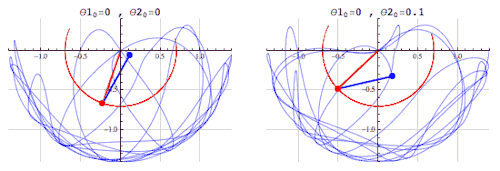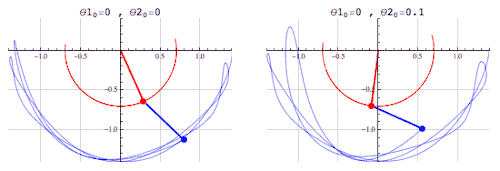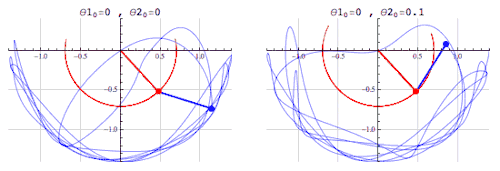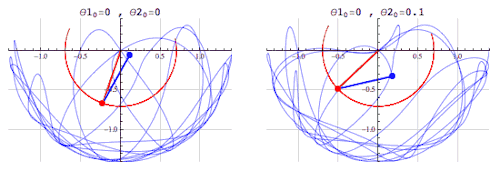
Esta ecuación describe un proceso en el tiempo. xt+1 es el nivel de alguna cantidad en un periodo dado. k es una constante. Para ciertos valores de k, el mapa muestra un comportamiento caótico: si empezamos en algún valor determinado inicial de x, el proceso evolucionará de una manera, pero si empezamos con otro valor inicial incluso uno muy cercano al primer valor, el proceso evolucionará muy distinto.
Vemos un comportamiento caótico en muchas áreas. El clima es un ejemplo clásico, un cambio pequeño en las condiciones atmosféricas un día, pueden llevar a sistemas completamente distintos unos días después. Se ejemplifica con el proverbio de que el aletear de una mariposa puede causar un huracán en otro continente.
17. Ecuación de Black-Scholes

Esta ecuación describe cómo los expertos en finanzas y comercio encuentran precios para derivados. Los derivados son productos financieros basados cuyo valor se basa en el precio de otro activo. El activo se llama activo subyacente. Estos pueden ser muy diferentes y son parte importante del sistema financiero moderno.
La ecuación permite a los profesionales calcular el valor, basados en propiedades de los derivados.